Deskewing LLS Data
Why do we need to deskew some LLS data? The lattice light-sheet microscope can create Z-stacks in 2 modes:
- Z Galvo stage and Z Piezo stage combination
- Sample Peizo stage
Z stacks created using the first mode are similar to those created on a typical confocal or widefield microscope and therefore don’t require deskewing. On the other hand, Z stacks created using the Sample Piezo stage do require deskewing. As is shown in Figure 1 below, a Z stack can be created by keeping the light-sheet stationary and dragging the sample through it using the sample Piezo stage.
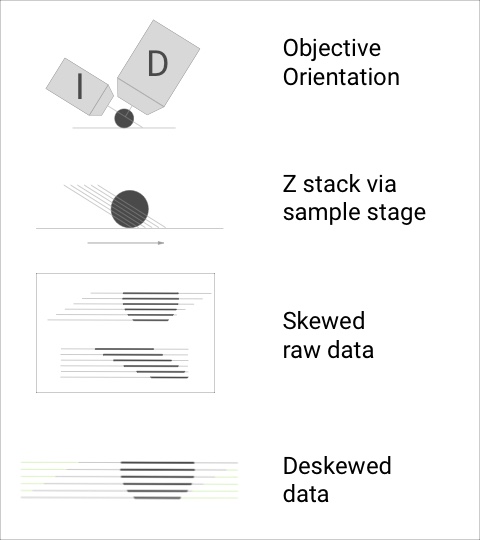
Figure 1: Schematic showing the skew introduced by creating Z-stacks using the Sample Piezo stage.
Implementation
Deskewing of LLS data is implemented using using a shear transform. Transforms are performed using the imglib2 library; however, the implementation provided by imglib2 currently only supports simple shear transforms with a shear factor of 1. Therefore, we implemented our own versions that allow shear transforms with arbitrary shear factors.
There are actually 2 versions available:
- Simple bounding box transform.
- Real view of data with interpolation combined with a bounding box transform.
One important consideration in deskewing LLS data is that the stage offsets used to generate Z sections are seldom divisible exactly by the physical size of a pixel in X (i.e., 101.8 nm), meaning that one cannot simply shear using whole pixel units. Therefore, a compromise is required, which can be broadly classified into two approaches:
- We could simply shift by the closest whole pixel unit to the stage offset.
- Interpolate the pixel data such that it can be resampled at the correct locations.
Interpolation schemes:
- None: No interpolation is performed; however, shear will be rounded to the nearest whole pixel.
- Nearest Neighbour: Transformed pixel value will be set to that of the nearest pixel.
- Linear
- Lanczos
Performance Characteristics
Performance of the deskewing is largely driven by the interpolation scheme used. The simple bounding box transform without interpolation is the fastest, although interpolation using a simple NearestNeighbour algorithms is only 1.42x slower in our measurements. Linear interpolation is about 7x slower than the bounding box transform, while Lanczos is orders of magnitude slower.
You can see the details of benchmarking here